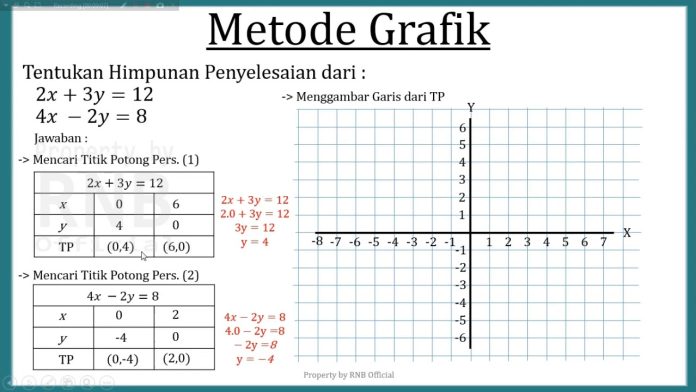
Cara Penyelesaian Soal Sistem Persamaan Linear Dua Variabel (SPLDV) Dengan Metode Grafik Lengkap, Berikut ini akan memberikan penjelasan lengkap tentang pengertian dan cara penyelesaian soal SPLDV dengan metode grafik.
Sistem persamaan linear dua variabel (SLDV) yaitu sebuah sistem / kesatuan dari beberapa persamaan linear dua variabel yang sejenis. Nah, kali ini kita akan membahas tentang cara menyelesaikan sistem persamaan linear dua variabel dengan metode grafik.
Dengan demikian, Simak berikut ini Cara Penyelesaian Soal Sistem Persamaan Linear Dua Variabel (SPLDV) Dengan Metode Grafik Lengkap yang dilansir dari berbagai laman dengan kumpulan penjelasan lengkap berikut ini:
Cara Menyelesaikan SPLDV Dengan Metode Grafik
Bagaimana bentuk grafik dari persamaan linear dua variabel? Grafik dari persamaan linear dua variabel berbentuk garis lurus, seperti yang ditunjukkan pada gambar berikut ini.
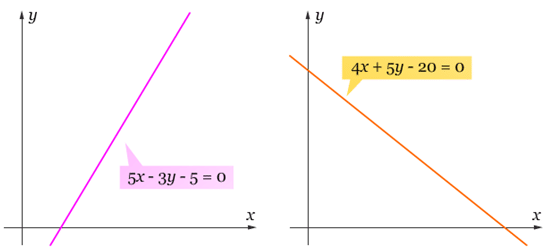
Lalu bagaimana cara menggunakan grafik persamaan linear tersebut untuk menyelesaikan permasalahan SPLDV? Pada dasarnya, terdapat 4 langkah dalam menyelesaiakan permasalahan SPLDV dengan menggunakan metode grafik. Keempat langkah tersebut antara lain:
- Memodelkan informasi yang ada di soal.
- Menentukan dua titik yang dilalui grafik persamaan-persamaan pada SPLDV.
- Menggambar sebuah grafik persamaan-persamaan tersebut.
- Menggunakan penyelesaian yang diperoleh untuk menjawab pertanyaan pada soal cerita.
Agar kalian lebih memahami, coba perhatika contoh soal berikut ini.
Dalam sebuah konser musik, terjual karcis kelas I dan kelas II sebanyak 500 lembar. Harga masing-masing karcis kelas I ialah Rp 8.000,00, sedangkan harga karcis kelas II ialah Rp 6.000,00. Jika hasil penjualan seluruh karcis tersebut adalah Rp 3.250.000,00, tentukanlah banyak karcis masing-masing kelas I dan kelas II yang terjual!
Langkah pertama yaitu mengubah kalimat-kalimat pada soal cerita tersebut menjadi model matematika, sehingga membentuk sebuah sistem persamaan linear. Misalkan banyak karcis I dan II yang terjual secara berturut-turut ialah x dan y, maka kalimat “Dalam sebuah konser musik, terjual karcis kelas I dan kelas II sebanyak 500 lembar,” bisa dimodelkan menjadi:
Sedangkan kalimat, “Harga karcis kelas I ialah Rp 8.000,00, sedangkan harga karcis kelas II ialah Rp 6.000,00. Jika hasil penjualan seluruh karcis ialah Rp 3.250.000,00,” bisa dimodelkan menjadi:
Sehingga diperoleh SPLDV seperti:
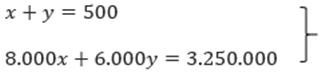
Langkah kedua adalah kita cari koordinat dua titik yang dilewati oleh grafik masing-masing persamaan tersebut. Biasanya, dua titik yang dipilih tersebut merupakan titik potong sebuah grafik persamaan-persamaan tersebut dengan sumbu-x dan sumbu-y.
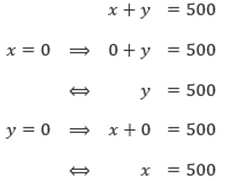
Sehingga grafik persamaan x + y = 500 memotong sumbu-x di (500, 0) dan memotong sumbu-y di (0, 500).
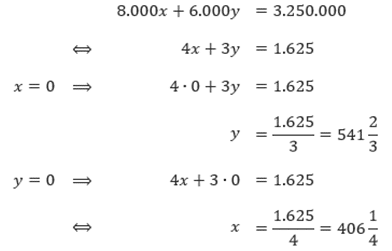
Sedangkan grafik 8.000x + 6.000y = 3.250.000 memotong sumbu-x di (406 1/4, 0) dan memotong sumbu-y di (0, 541 2/3).
Langkah ketiga adalah kita gambarkan sebuah grafik persamaan-persamaan tersebut pada koordinat Cartesius. Grafik persamaan-persamaan tersebut bisa dilukis dengan memplot titik-titik yang sudah kita cari pada koordinat Cartesius kemudian hubungkan titik (500, 0) dan (0, 500) untuk mendapatkan grafik x + y = 500, serta titik (406 1/4, 0) dan (0, 541 2/3) untuk mendapatkan grafik 8.000x + 6.000y = 3.250.000.
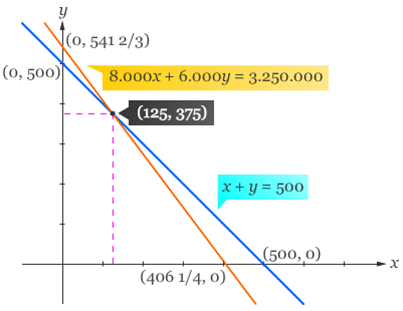
Dari grafik di atas tersbut diperoleh bahwa titik potong grafik x + y = 500 dan 8.000x + 6.000y = 3.250.000 ialah (125, 375). Sehingga selesaian dari SPLDV di atas yaitu x = 125 dan y = 375.
Langkah keempat adalah kita gunakan selesaian di atas untuk menjawab pertanyaan pada soal cerita. Karena x dan y secara berturut-turut menyatakan bahwa banyak karcis I dan II yang terjual, maka banyaknya karcis kelas I yang terjual ialah 125 lembar dan 375 lembar untuk karcis kelas II.
Itulah penjelasan lengkap dari Cara Penyelesaian Soal Sistem Persamaan Linear Dua Variabel. Semoga Bermanfaat!
 Dengan Metode Grafik Lengkap, Berikut ini akan memberikan penjelasan lengkap tentang pengertian dan cara penyelesaian soal SPLDV dengan metode grafik.){kind=link}