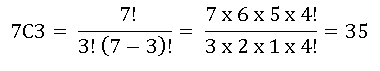Hallo teman-teman kali ini kita semua kan membahas tentang Contoh soal Peluang dan Pembahasan lengkap dengan kunci jawabannya. Simak berikut ini!
Contoh Soal Peluang Dan Pembahasan
1.) Ada sebuah dadu lalu dilempar sekali, tentukan peluang munculnya mata dadu 6!
Jawab :
Banyaknya titik sampel n(s) = 6
Titik sampel dadu bernilai 6 n(A) = 1
Jawab :
Banyaknyaa titik sampel n(s) = 4 + 3 + 5 = 12
Titik sampel kelereng biru n(A) = 3
Jawab :
Ruang sampelnya yakni = { (A,G), (A,A), (G,A), (G,G)}
n ( s) = 4
banyaknya titik sampel keduanya angka yakni n (A) = 1
Peluang kejadian
Besarnya kemungkinan terjadinya sebuah kejadian disebut peluang kejadian. Penentuan nilai dari peluang kejadian didasarkan pada banyak anggota dan banyak anggota ruang sampelnya. Jika secara matematis penentuan nilai peluang suatu kejadian ditulis:
PK = nK / nS
Catatan:
- Agar dapat menentukan nK atau nS dapat menggunakan rumus permutasi atau Kombinasi:
- Permutasi dipakai jika dalam soal ada istilah jabatan, urutan, rangking, predikat, cara duduk, susunan angka.
- Kombinasi digunakan jika dalam soal ditanyakan: banyak himpunan bagian, peluang, urutan diabaikan.
4.) Pada pelemparan dua dadu setimbang bersamaan. Misalnya K adalah kejadian muncul jumlah mata dadu = 6. Peluang kejadian K adalah…
A. 8 / 36
B. 7 / 36
C . 6 / 36
D. 5 / 36
E. 4/36
Pembahasan
nK = 5
nS = 36
Jawaban: D
5.) Dalam sebuah kotak terdapat 7 kelereng merah dan 3 kelerang biru. Peluang mengambil 3 kelereng merah sekaligus….
B. 1/3
C. 7/24
D. 1/4
E. 3/7
Pembahasan
Cara agar terambilnya 3 kelereng merah dari 7 kelereng merah = nK = 7C3.
Banyak cara agar teraambil 3 kelereng merah dari seluruh kelereng 10 buah = nS = 10C3
Peluang terambil 3 kelereng merah nK.
6.) Dalam sebuah kantong terdapat 7 kelereng merah dn 4 kelereng putih. Akan diambil 4 kelereng sekaligus. Peluang terambiilnya 2 kelereng merah dan 2 kelereng putih adalah…
A. 126/330
B. 116/330
C. 63/330
D. 53/330
E. 27/330
Cara agar terambilnya 2 kelereng merah dari 7 kelereng = 7C2.
7C2 = 7! / (2! . 5!) = 21.Cara agar terambilnya 2 kelereng putih dari 4 kelereng = 4C2.
4C2 = 4! / (2! . 2!) = 6.Cara agar terambilnya 2 kelereng merah dan 2 kelereng putih = nK = 7C2 . 4C2 = 21 . 6 = 126.
Cara agar terambilnya 4 kelereng dari seluruh kelereng (11 kelereng) = nS = 11C4.
Peluang terambilnya 2 kelereng merah dan kelereng putih PK.
PK = 126/330.
Jawaban: A
7.) Dua dadu dilambungkan bersama-sama. Peluang munculnya mata dadu yang pertama 3 dan mata dadu kedua lima adalah…
A. 6 / 36
B. 5 / 36
C. 4 / 36
D. 3 / 36
E. 1 / 36
Jawaban:
Merupakan peluang kejadian saling lepas:
P(3 dan 5) = P(3) x P(5) = 1/6 x 1/6 = 1 / 36
8.) Jika sebuah dadu dan sekeping mata uang dilempar undi satu kali bersama, maka peluang untuk memperoleh GAMBAR pada mata uang dan bilangan ganjil pada dadu adalah…
A. 1/12
B. 1/6
C. 1/4
D. 1/3
E. 1/2
Pembahasan
Merupakan peluang saling bebas, maka:
P(gambar dan ganjil) = P(gambar) x P(ganjil) = 1/2 x 3/6 = 3/12 = 1/4
Catatan
P(gambar) = nK / nS = 1/2
P(ganjil) = nK / nS = 3/6
9.) Dua buah dadu dilempar undi bersama-sama. Peluang munculnya jumlah mata dadu 9 atau 10 ,yaitu …
A. 5 / 36
B. 7 / 36
C. 8 / 36
D. 9 / 36
E. 11 / 36
Pembahasan
Merupakan peluang kejadian saling lepas:
P (9 atau 10) = Peluang(9) + Peluang(10) = 4/36 + 3/36 = 7/36
Keterangan
nS (2 dadu) = 36
nK (9) = (3,6), (6,3), (4,5), (5,4) = 4
nK (10) = (4,6), (6,4), (5,5) = 3
Jadi:
P(9) = nK / nS = 4/36
P(10) = nK / nS = 3/36
10.) Pada percobaan pelemparan sebuah mata uang logam sebanyak 150 kali, ternyata muncul angka sebanyak 78 kali. Tentukanlah
a. Frekunsi munculnya angka
b. Prekunesi munculnya gambar
Penyelesaian :
a. Frekuensi relatif yang akan muncul angka = banyak angka yang muncul banyak percobaan
= 78 / 150
= 13/25
b. Frekuensi relatif yang akan muncul gambar = banyak gambar yang muncul banyak percobaan
= (150-78)/150
= 72/150
= 12/25
11.) Dalam sebuah kotak terdapat lima buah bola yang diberi nomor 1 sampai 5. Jika bola ingin diambil secara acak dari kotak tersebut.
a. Tentukanlah peluang terambilnya bola bernomor gelap.
b. Jika yang terambil adalah bola bernomor ganjil, serta tidak dikembalikan lagi. Tentukanlahlah peluang terambilnya bola bernomor ganjil pada saat pengambilan berikutnya.
Penyelesaian :
a. Banyaknya bola bernomor genap ada 2 yaitu bola bernomor 2 dan 4.
Sehingga P(genap) = 2/5
b. Banyaknya bola bernomor ganjil ada 3, terambil 1 sehingga banyak bola bernomor ganjil sekarang 2.
Maka P(ganjil) = (3-1)/(5-1) = 2/4 = 1/2
12.) Apabila terdapat sebuah dadu yang dilempar undi sekali, tentukanlah peluang muncul :
a. mata dadu 4
b. mata dadu bilangan ganjil
Penyelesaian :
a. Banyaknya kejadian yang muncul mata dadu 4 = 1. Banyak kejadian yang mungkin muncul = 6 yaitu muncul mata dadu 1, 2, 3, 4, 5 dan 6.
Sehingga, P(mata 4) = 1/6
b. Banyaknya kejadian yang akan muncul mata dadu bilangan ganjil = 3 yaitu mata dadu 1, 3, dan 5.
Sehingga, P(ganjil) = 3/6 = 1/2
13.) salah satu huruf dipilih secara acak dari huruf-huruf pada kata ” SURABAYA”. Tentukanlah peluang terpilihnya huruf A?
Penyelesaian :
banyaknya kejadian muncul huruf A = 3 karena terdapat 3 huruf pada kata tersebut.
banyak kejadian yang mungkin = 8
Sehingga, P(huruf A)= 3/8.
Demikianlah ulasan kami mengenai contoh soal peluang, Semoga bermanfaat!
 Ada sebuah dadu lalu dilempar sekali, tentukan peluang munculnya mata dadu 6!){kind=link}