Contoh Soal Persamaan Nilai Mutlak Lengkap Pengertian, Sifat, Konsep dan Lainnya, Nilai Mutlak Merupakan suatu bilangan yang riil tanpa tanda atau minus dalam linear dengan satu variabel tidaklah yang sulit sehingga memiliki konsep yang dinamakan nilai mutlak dengan sifat persamaan dalam penyelesaian satu variabel.
Dilansir dari laman Materibelajar.co.id, berikut ini penjelasan lengkap dari Contoh Soal Persamaan Nilai Mutlak Lengkap Pengertian, Sifat, Konsep dan Lainnya
Pengertian Nilai Mutlak
Nilai Mutlak Merupakan suatu bilangan yang riil tanpa tanda atau minus dalam linear dengan satu variabel tidaklah yang sulit sehingga memiliki konsep yang dinamakan nilai mutlak dengan sifat persamaan dalam penyelesaian satu variabel.
Dalam nilai mutlak ini cukup di lakukan dengan cara yang serupa sehingga dapat bertindak seperti aljabar yang ekuivalen dengan satu variabel yang sama sebagai sifat untuk menentukan penyelesaian yang diberikan.
Sifat Nilai Mutlak
Dari penjelasan yang singkat di atas maka dalam mengambil nilai mutlak ini dari persamaan nilai ternyata sangatlah mudah dengan mengikuti beberapa variabel yang ada, dan aturan yang telah dibahas untuk menentukan nilai mutlaknya.
Shingga nilainya dapat berfungsi yang positif dan memiliki fungsi di dalam tanda yang sama lebih dari nilai nol yang riel dan dapat menjadi dan bernilai negatif.
Konsep Nilai Mutlak
Konsep yang terdapat dalam persamaan nilai ini yang terdapat dalam contoh adalah pada kehidupan sehari-hari dengan menggambarkan sebuah pemimpin barisan pramuka untuk memerintah yang maju, Maka dapat melewati jarak dengan pergerakan barisan pemerintah yang besar hingga pegerakan barisan diatas.
Persamaan Nilai Mutlak Satu Variabel
Sebuah garis bilangan akan digunakan sebagai alat media untuk menunjukan beberapa nilai mutlak dengan besaran nilai mutlak yang dilihat dari panjang tanda panah.
Sedangkan tanda panah tersebut dapat juga digunakan untuk menentukan besaran nilai mutlak dalam arah ke kiri yang menandakan nilai mutlak dari bilangan yang negatif,
Dan begitu sebaliknya juga arah ke kanan dapat menandakan nilai mutlak dari sebuah bilangan yang positif.
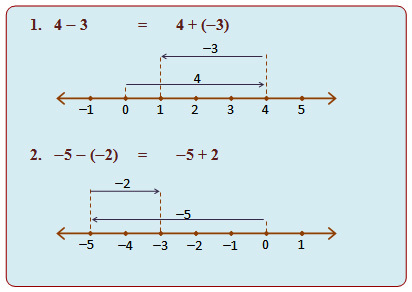
Perhatikan ilustrasi di bawah ini :
Tanda panah akan bergerak dari bilangan 0 dengan menuju ke arah kanan dan pada bilangan 3 maka besaran langkah yang di lewati sebagai tanda panah – 3 dari satuan bilangan 0.
Tanda panah dapat bergerak dari bilangan 0 dengan menuju ke arah bilangann kiri -3 dengan besaran langkah yang di lewati tanda panah 3 dari satuan bilangan 0.
Contoh Soal Persamaan Nilai Mutlak
Dari penjelasan di atas maka di sini juga kami akan memberikan beberapa contoh soal tentang apa materi dari pembahan ini dan semoga dari contoh ini dapat berguna.
Berikut contoh soal tentang Persamaan Nilai Mutlak adalah sebagai berikut :
Soal 1
Tentukanlah himpunan dari penyelesaian -3x +7 = 3
Jawab
Berdasarkan dari sifatnya maka:
- 3x-7= 3-3x +7 = 3 atau 3x – 7 = -3
- 3x-7= 3-3x = 10 atau 3x = 4
- 3x-7= 3- = 5 atau x = 3
Sehingga himpunan tersebut dapat di selesaikan adalah HP = {3-5}
Soal 2
Tentukanlah himpunan dari 3x +1= x-4
Jawab
Berdasarkan dari sifatnya maka
3x-1 = x + 4
- 3x+1 = x + 4 atau 3x – 1 = (x + 4)
- x =- 5 atau 4x =4
- x = -5 atau x =1
Sehingga himpunan tersebut adalah HP = {1- 5}
Langkah Langkah Menyelesaikan Nilai Mutlak
Dalam menyelesaikan dari persamaan nilai mutlak yang mengandung dalam menghitung antara jarak pada suatu angka dan mengukur jarak x dari nol dengan nilai riel, maka bisa ditemukan dalam kondisi batasan sehingga dapat selesaikan dari berbagai jenis-jenis pertidakan nya melalui cara evaluasi.
Langkah 1 adalah dengan cara Evaluasi pada bentuk pertidaksamaan dengan nilai mutlak yang sudah dinotasikan dengan X
Maka salah satu nya adalah sebagai berikut :
x < a atau x> a x±a < b atau x±a > b ax2+bx- < c
pada fokusnya ialah dengan bentuk f(x) – < a dan f(x)> a atau f- (x) berupa fungsi yang kosntanta.
Langkah 2 merupakan dengan cara dapat mengubah pertidaksamaan nilai mutlak dengan menjadi pertidaksamaan yang biasa dengan pertidaksamaan -x < 3 atau dengan x < -3
Contohnya
- x−3>5 jadi – (x+ 3) > 5 atau x-3 > 5
- 3x+2 < 5 jadi – (3x-2) < 5 atau 3x-2 < 5
Langkah 3 merupakan dengan cara nilai x seperti angka negatif untuk menyendirikan -x ke salah satu sisi.
Contohmya
- jika dalam membagi dari kedua sisi misal -1+ -x > 5 menjadi x <+5
Langkah 5 merupakan dengan cara untuk himpunan dengan penyelesaian dari nilai x dengan jangkauan nilai yang sering mempunyai dua penyelesaian.
Perhatikan pada contoh di bawah ini:
- 7-3 < x < 1
- 7-3+1)