Fungsi Linear: Rumus, Penjelasan dan Grafik

Titik potong dua buah garis

Menentukan titik potong dari dua buah garis lurus identik dengan menyelesaikan permasalahan dari sistem persamaan liniear dua variabel, baik dengan metode eleminiasi, metode substitusi atau metode grafik.

Hubungan dua buah garis

Dua garis yang bergradien m1 dan m2 dapat disebut sejajar apabila m1 = m2 dan tegak lurus apabila m1xm2 = -1

Berimpit

Dua garis lurus akan berimpit apabila persamaan garis yang satu adalah kelipatan dari garis lainnya. Dengan demikian garis y1 = a1 + b1x akan berimpit dengan garis y2 = a2 + b2x, apabila y1 = ny2 a1 = na2 b2 = nb2

Sejajar

Dua garis lurus akan sejajar, jika gradien garis yang satu sama dengan gradien dari garis yang lain. Maka dari itu, garis y1 = a1 + b1x akan sejajar dengan garis y2 = a2 +b2x, apabila b1 = b2 .

Berpotongan

Dua garis lurus akan berpotongan jika gradien yang satu tidak sama dengan gradien garis yang lain. Maka dari itu, garis y1 =a1 + b1x akan berpotongan dengan garis y 2 = a2 + b2x, apabila b1 b2.

Tegak lurus

Dua garis lurus akan saling tegak lurus apabila gradien garis yang satu adalah kebalikan dari gradien garis lainnya dengan tanda yang berlawanan. Maka dari itu, garis y1 =a1 + b1x akan tegak lurus dengan garis y2 = a2 + b2 x, apabila atau b1 = -2.

B. Grafik Fungsi Linear dan Contohnya

B1. Cara Membuat Grafik Fungsi Linear

Berikut beberapa langkah untuk membuat grafik fungsi linear dalam koordinat kartesius

1. Mengidentifikasi fungsi linear
   • Apakah fungsi termasuk linear?
   • Apakah fungsi sudah sesuai dengan bentuk umum fungsi linear?
   • Jika belum, ubah persamaan ke bentuk umum fungsi linear
2. Merancang grafik fungsi linear
   • Apakah fungsi mempunyai konstanta c?
     • Jika tidak, maka c = 0 dan grafik fungsi memotong titik pusat koordinat kartesius di (0, 0)
     • Jika ya, maka fungsi memotong sumbu y dengan nilai c
   • Apakah fungsi mempunyai variabel bebas (ax)?
     • Jika tidak mempunyai variabel bebas maka grafik akan berbentuk horizontal
       • a = 0, tidak miring (horizontal)
     • Jika mempunyai variabel bebas, maka kemiringan grafik (gradien) ditentukan oleh nilai a dalam bentuk umum y = ax + b ⇔ y = mx + b
       • • m < 0, miring ke kiri
         • m > 0, miring ke kanan

        

   • Lakukan substitusi ke model fungsi minimal 2 nilai bebas
3. Menggambar Grafik
   • Menandai titik rancangan grafik
     • Titik Potong
     • Dan titik hasil substitusi
   • Menarik garis dari titik-titik yang telah ditandai

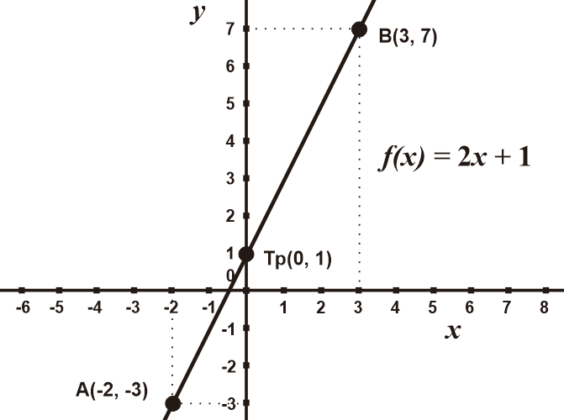
Contoh 1: Grafik Fungsi f(x) = 2x + 1

# Identifikasi fungsi linear f(x) = 2x + 1
Fungsi termasuk linear, karena terdiri dari konstanta dan suku berderajat satu
Fungsi sudah sesuai dengan bentuk umum fungsi linear

# Perancangan grafik f(x) = 2x + 1
Mempunyai nilai c = 1, sehingga titip potong sumbu y di titik Tp(0, 1)
Mempunyai koefisien a = 2, sehingga m > 0 dan grafik miring ke kanan
Substitusi nilai acak misalnya diambil nilai acak -2 dan 3 diperoleh

f(x) = 2x + 1 
  y  = 2x + 1

f(-2) = 2(-2) + 1
      = -3
Diperoleh titik A(x, y) = A(-2, -3)

f(2) = 2(3) + 1
     = 7
Diperoleh titik B(x, y) = B(3, 7)

# Menggambar grafik f(x) = 2x + 1

Sehingga dapat dibuat grafik berikut dalam koordinat kartesius