Fungsi Linear: Rumus, Penjelasan dan Grafik

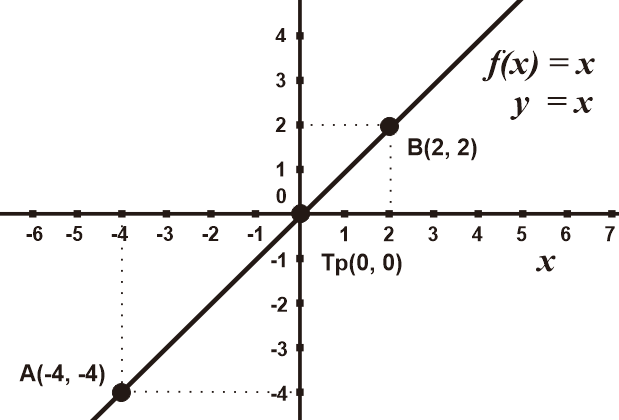
Contoh 2: Grafik Fungsi y = x

# Identifikasi fungsi y = x
Fungsi termasuk linear, karena tersusun dari suku berpangkat 1
Fungsi sudah sesuai dengan bentuk umum fungsi linear y = x ⇔ f(x) = x

# Perancangan grafik fungsi y = x
Tidak mempunyai nilai c atau c = 0, sehingga grafik memotong titik koordinat Tp(0, 0)
Mempunyai koefisien a = 1, sehingga m > 0 dan grafik miring ke kanan
Substitusi nilai acak misalnya diambil nilai acak -4 dan 2 diperoleh

      y = x
⇔ f(x) = x

f(-4) = x
      = -4
Diperoleh titik A(x, y) = (-4, -4)

f(2) = x
     = 2
Diperoleh titik B(x, y) = (2, 2)

# Menggambar fungsi y = x

Sehingga dapat dibuat grafik berikut dalam koordinat kartesius

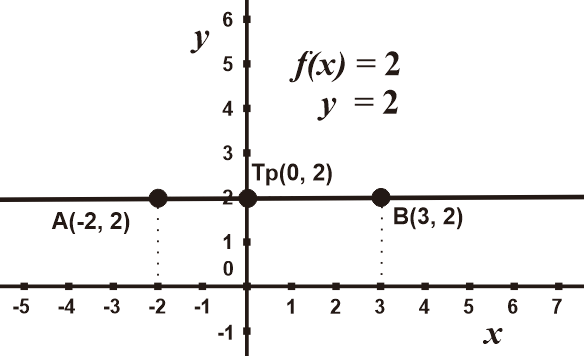
Contoh 3: Grafik Fungsi y = 2

#Identifikasi fungsi y = 2
Fungsi termasuk linear karena tersusun dari konstanta
Fungsi sudah sesuai dengan bentuk umum fungsi linear y = 2 ⇔ f(x) = 2

# Perancangan grafik fungsi y = 2
Fungsi mempunyai nilai c = 2, sehingga grafik memotong sumbu y di Tp(0, 2)
Fungsi tidak mempunyai variabel bebas, sehingga nilai a = 0 dan grafik berbentuk horizontal
Substitusi nilai acak misalnya diambil nilai acak -2 dan 3 diperoleh

      y = 2
⇔ f(x) = 2

f(-2) = 2
Diperoleh titik A(-2, 2)

f(3) = 2
Diperoleh titik B(3, 2)

∴ Dapat diketahui semua nilai yang disubstitusikan akan bernilai 2

# Menggambar fungsi y = 2

Sehingga dapat dibuat grafik berikut dalam koordinat kartesius

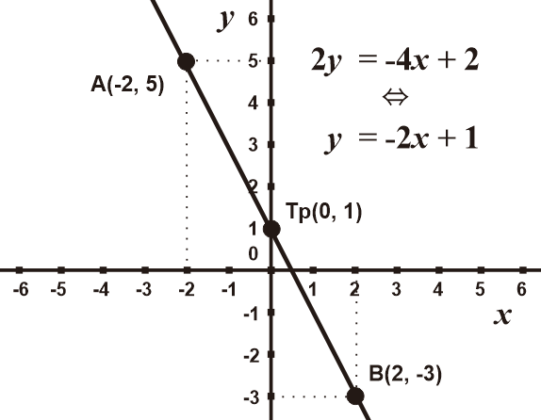
Contoh 4: Grafik Fungsi 2y = -4x + 2

# Identifikasi fungsi 2y = -4x + 2
Fungsi merupakan linear karena tersusun oleh konstanta dan suku berderajat satu
Fungsi belum memenuhi bentuk umum fungsi linear, karena ruas kanan untuk variabel y mempunyai koefisien bukan satu

Sehingga untuk merancang grafik, fungsi diubah ke dalam bentuk umum fungsi linear

   2y =  -4x + 2
⇔  y =  -4x + 2 
            2
⇔  y =  -2x + 1
 f(x) =  -2x + 1

Sehingga bentuk umum fungsi linear dari 2y = -4x + 2 adalah f(x) = -2x + 1

# Perancangan grafik fungsi dalam bentuk umumnya f(x) = -2x + 1
Bentuk umum mempunyai nilai c = 1, sehingga grafik fungsi memotong sumbu y di Tp(0, 1)
Bentuk umum mempunyai koefisien a = -2, sehingga m < 0 dan grafik miring ke kiri
Substitusi nilai bebas, misalnya -2 dan 2 diperoleh

2y = -4x + 2
⇔ y = -2x + 1
f(x) = -2x + 1

f(-2) = -2(-2) + 1
      = 4 + 1
      = 5
Diperoleh titik A(-2, 5)

f(2) = -2(2) + 1
     = -4 + 1
     = -3
Diperoleh titik B(2, -3)

# Menggambar grafik fungsi dalam bentuk umumnya

Sehingga diperoleh gambar grafik berikut