Jaring-Jaring Kubus Lengkap Pengertian, Sifat, Unsur dan Pembahasan Rumus

Jaring-Jaring Kubus Lengkap Pengertian, Sifat, Unsur dan Pembahasannya, Berikut akan membahas tentang Kubus dilengkapi dengan penjelasan lengkap dari sifat-sifat kubus, unsur-unsurnya dan pembahasan jaring-jaring Kubus.

Dengan demikian, Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang kongruen berbentuk bujur sangkar atau persegi. Ciri-ciri  kubus memiliki 6 sisi, 12 rusuk, dan 8 titik sudut.

Simak berikut lengkap Jaring-Jaring Kubus Lengkap Pengertian, Sifat, Unsur dan Pembahasannya.

Jaring-Jaring Kubus Lengkap Pengertian, Sifat, Unsur dan Pembahasannya

Sifat-Sifat Kubus

• Semua sisi kubus berbentuk persegi
• Semua rusuk kubus beukuran sama panjang
• Setiap diagonal bidang pada kubus memiliki ukuran yang sama panjang.
• Setiap diagonal ruang pada kubus memiliki ukuran yang sama panjang.
• Setiap bidang diagonal pada kubus memiliki bentuk persegi panjang.

Unsur-Unsur Kubus

Sisi atau Bidang Kubus
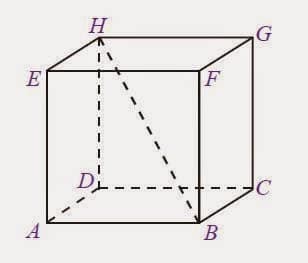
Sisi atau Bidang Kubus adalah Bidang atau sisi yang membatasi Kubus. Kubus memiliki 6 sisi. Perhatikan gambar kubus diatas, yang merupakan sisi atau bidang kubus yaitu (ABCD), (EFGH), (ABFE), (DCGH), (BCGF), dan (ADHE).

Rusuk
Rusuk adalah garis potongan antar dua sisi bidang kubus dan terlihat seperti kerangka yang menyusun kubus. Kubus mnemiliki 12 rusuk. Perhatikan gambar kubus diatas, yang merupakan Rusuk yaitu AB, BC, CD, DA, AE, BF, CG, DH, EF, FG, GH, dan HE.

Titik Sudut
Titik Sudut adalah titik potongan antara dua atau 3 rusuk. Kubus memiliki 8 titik sudut. Perhatikan gambar kubus diatas, yang merupakan Titik Sudut yaitu A, B, C, D, E, E, F, G, dan H.

Diagonal Bidang atau Diagonal Sisi
Diagonal Bidang atau Diagonal Sisi adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan pada setiap bidang atau sisi kubus. Kubus memiliki 12 diagonal sisi atau diagonal bidang. Sekarang coba perhatikan bidang ABEF pada gambar kubus ABCD.EFGH di bawah ini.

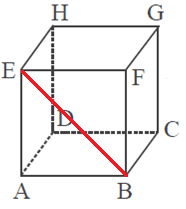
Yang merupakan diagonal bidang diantaranya : AF, BE, BG, CF, CH, DG, DE, AH, AC, BD, EG, dan HF. Diagonal bidang atau sisi dapat ditentukan dengan menggunakan teorema phytagoras. Sekarang perhatikan gambar kubus di bawah ini.

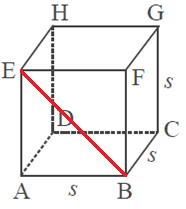
Bagaimana cara menghitung panjang diagonal bidang atau diagonal sisi pada kubus? Misalkan kubus ABCD.EFGH di atas memiliki rusuk s. Maka panjang BE dapat dihitung dengan menggunakan teorema phytagoras, di mana segitiga ABE siku-siku di A. Sehingga:

BE = √(AB² + AE²)
BE = √(s² + s²)
BE = √2s²
BE = s√2

Misalkan diagonal bidang kubus adalah b maka secara umum diagonal bidang kubus dapat dirumuskan:
b = s√2

Diagonal Ruang
Diagonal Ruang adalah garis yang menghubungkan 2 titik sudut yang saling berhadapkan dalam satu ruang. Kubus memiliki 4 diagonal ruang. Perhatikan gambar kubus dibawah ini.

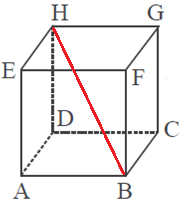
Yang merupakan diagonal ruang adalah AG , BH , CE , dan DF .

Bagaimana menghitung panjang diagonal ruang kubus? Sama seperti mencari diagonal bidang, untuk mencari diagonal ruang juga menggunakan teorema phyagoras. Sekarang perhatikan gambar di bawah ini.

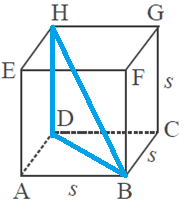
Misalkan kubus ABCD.EFGH di atas memiliki rusuk s. Maka panjang BH dapat dihitung dengan menggunakan teorema phytagoras. Tetapi sebelum itu harus cari panjang BD, di mana BD merupakan diagonal sisi. Sekarang perhatikan segitiga ABD siku-siku di A. Sehingga:
BD = s√2

Sekarang cari panjang BH dengan teorema phytagoras juga. Sekarang perhatikan segitiga BDH siku-siku di D. Sehingga:

BH = √(BD² + DH²)
BH = √(s√2)² + s²)
BH = √(2s² + s²)
BH = √(3s²)
BH = s√3

Misalkan diagonal ruang kubus adalah d, maka secara umum diagonal ruang kubus dapat dirumuskan:
d = s√3

Bidang Diagonal Kubus
Bidang diagonal suatu kubus adalah bidang yang dibatasi oleh dua rusuk dan dua diagonal bidang suatu kubus. Terdapat 6 Bidang diagonal pada Kubus. Perhatikan gambar dibawah ini:

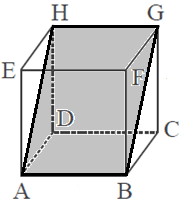
Bidang ABGH disebut bidang diagonal, selain itu yang merupakan bidang diagonal yaitu ACGE, AFGD, CDEF, BFHD, dan BEHC. Bagaimana menghitung luas bidang diagonal?

Untuk menghitung luas bidang diagonal dapat menggunakan rumus luas persegi panjang. Sekarang coba perhatikan kembali gambar kubus ABCD.EFGH di atas, jika rusuknya s, maka luas bidang ABGH yakni:
Luas ABGH = AB . BG
Luas ABGH = s . s√2
Luas ABGH = s²√2

Jaring-Jaring Kubus

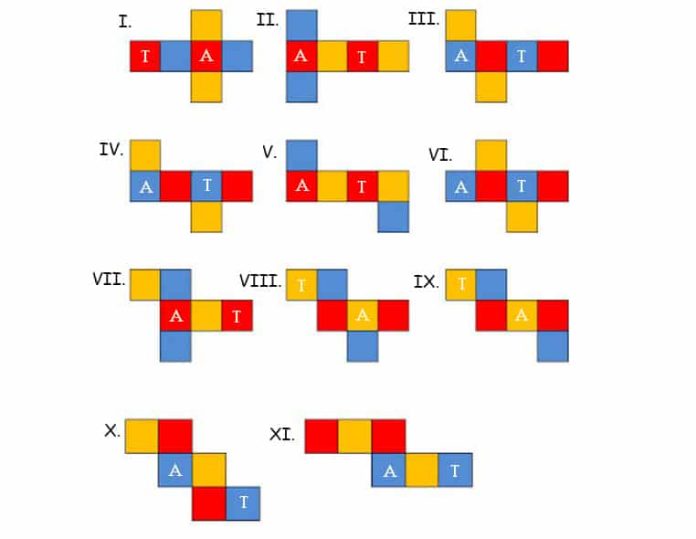
Jaring-Jaring adalah bidang datar yang berupa gabungan dari bangun datar yang membentuk sebuah bangun ruang seperti kubus, balok, limas dan lain sebagainya. Jaring-jaring bisa didapatkan dengan cara membagi sebuah bangun ruang dengan mengikuti rusuk-rusuknya. Kali ini kita akan membahas tentang bentuk jaring-jaring kubus. Jaring-jaring kubus terdiri dari 6 buah bangun datar persegi atau bujur sangkar. Berikut adalah Jaring-Jaring Kubus:

Keterangan:

A : Alas
T : Tutup