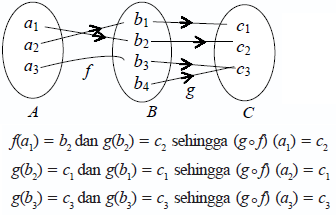
Latihan Soal Dan PembahasanFungsi Komposisi, Aljabar Fungsi dan Komposisi Fungsi Lengkap

Latihan Soal Dan Pembahasan Fungsi Komposisi, Aljabar Fungsi dan Komposisi Fungsi Lengkap, Kali ini pelajaran sekolah akan kembali membahas tentang latihan soal dari Fungsi Komposisi, Aljabar Fungsi dan Komposisi Fungsi Lengkap.

Latihan soal di bawah ini bisa menjadi referensi dan contoh dalam mengerjakan soal-soal agar lebih mudah dan gampang. Simak di bawah ini..

Latihan Soal Dan Pembahasan

1. Diketahui fungsi f : R → R dan g : R → R dengan rumus f(x) = x + 1 dan

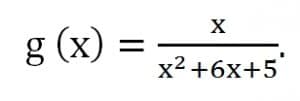
Tentukan :

a. Daerah asal g(x)
b. Rumus fungsi (fₒg)(x)
c. Rumus fungsi (gₒf)(x)

Penyelesaian

a.

agar bernilai real, x + 1 ≠ 0 atau x + 5 ≠ 0.
x + 1 ≠ 0 → -1
x + 5 ≠ 0 → -5

Jadi, daerah asal g (x) adalah {x | x ≠ -5, x ≠ -1, x € R}.

b.

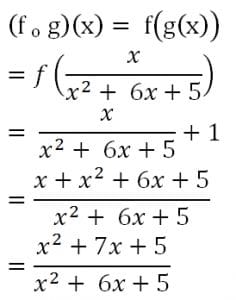
Jadi, rumus fungsi 

c.

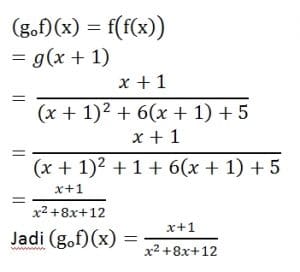
2. Jika f(x)= x² – 2x + 2 dan g (x) = x + 1 , tentukan :

a. Rumus fungsi (f ₒ g) (x)
b. Nilai a agar (g ₒ f) (a) = 2

Penyelesaian

a. (f ₒ g) (x) = (f (g) (x))
= f ( x + 1 )
= (x + 1)² – 2(x+1) + 2
= x² + 2x + 1 – 2x – 2 + 2
= x² + 1

Jadi, rumus fungsi (f ₒ g) (x) = x² + 1

b. (g ₒ f)(x) = g(f(x))
= g (x² – 2x + 2)
= x² – 2x + 2 + 1
= x² – 2x + 3

(g ₒ f) (a) = 2
→ a2 – 2a + 3 = 2
→ a2 – 2a + 1 = 0
→ (a – 1)² = 0
→ a – 1 = 0
→ a = 1

Jadi, nilai a = 1

3. Diketahui ( f ₒ g) (x + 2) = 12x – 5 dan f (x) = 6x + 1. Tentukan

a. g (x)
b. (g ₒ f) (x – 1)

Jawaban

a. Misalkan x + 2 = t → x = t – 2
(g ₒ f) (x + 1) = 12x – 5
→ (f ₒ g) (t) = 12 (t – 2) – 5
→ (f ₒ g) (t) = 12t – 24 – 5
→ (f ₒ g) (t) = 12t – 29
→ (f ₒ g) (t) = 12x – 29

(f ₒ g)(x) = f(g)(x))
→12x – 29 = 6g(x) + 1
→ 6g(x) = 12x – 30
→ g(x) = 2x – 5

Jadi, g(x) = 2x – 5

b. (g ₒ f) (x) = g (f(x))
= g (6x +1)
= 2 (6x + 1) – 5
= 12x – 3

(g ₒ f) (x – 1) = 12 (x – 1) – 3
= 12x – 15

Jadi, (g ₒ f) (x – 1) = 12x – 15

4. Diketahui f(x) = 5x – 3 dan g (x – 2) = 2x + 3. Tentukan :

a. Rumus fungsi g (x)
b. h (x) jika diketahui (h ₒ g) (x) = 6x + 23

jawaban

a. Misalkan t = x – 2 → x = t + 2
g (x – 2) = 2x + 3
→ g (t) = 2 (t + 2) + 3
→ g (t) = 2t + 4 + 3
→ g (t) = 2t + 7
→ g (x) = 2x + 7

Jadi, rumus fungsi g (x) = 2x + 7

b. Misalkan g(x) = t = 2x + 7 → ^t-7/₂
(h ₒ g)(x) = 6x + 23
→ h (g(x)) = 6x + 23
→h(2x + 7) = 6x + 23
→ h (t) = 6 (^t-7/₂) + 23
→ h (t) = 3 (t – 7) + 23
→ h (t) = 3t + 2
→ h (x) = 3x + 2

Jadi, h (x) = 3x + 2

Latihan soal!

Tentukan bentuk fungsi asal.

Diketahui f (x+1) = 4x + 1 dan (f ₒ g) (x) = 12x – 23 . Dapatkah kamu menentukan f(x) dan g (x)? ikuti dan lengkapilah cara berikut.

1. Misalkan t = x + 1 sehingga x = …. – 1

F (x + 1) = 4x + 1
→ f (t) = 4 (t – … ) + 1
→ f (t) = 4 t – …  + 1
→ f (t) = 4t – …

Dengan mengganti t pada f(t) = 4t – 3 dengan x, diperoleh f(x) = 4x – 3. Jadi, f(x) = 4x – 3.

2. (f ₒ g) (x) = 12x – 23

→ f (g(x)) = 12x – 23
→ 4g (x) – 3 = 12x – 23
→4g (x) = 12x – 23 + ….
→ 4g (x) = 12x – ….
→ g (x) = 3x – 5

Jadi, g(x) = 3x -5.

Itulah Latihan Soal Dan PembahasanFungsi Komposisi, Aljabar Fungsi dan Komposisi Fungsi Lengkap, Semoga Bermanfaat!!