Pengertian Barisan Geometri Lengkap Rumus, Contoh Soal dan Rumus deret Geometri

Pengertian Barisan GeometriLengkap Rumus, Contoh Soal dan Rumus deret Geometri, Berikut akan kembali membahas tentang Barisan Geometri dan deret geometri lengkap dengan rumus dan contoh soal masing-masing.

Dengan demikian dilansir dari berbagai laman simak berikut ini penjelasan dari Pengertian Barisan GeometriLengkap Rumus, Contoh Soal dan Rumus deret Geometri. Barisan Geometri dapat didefinisikan sebagai barisan yang tiap-tiap sukunya diperoleh dari hasil perkalian suku sebelumnya dengan sebuah konstanta tertentu.

Rumus Barisan Geometri

Barisan Geometri dapat didefinisikan sebagai barisan yang tiap-tiap sukunya diperoleh dari hasil perkalian suku sebelumnya dengan sebuah konstanta tertentu.

Barisan geometri adalah barisan yang emmenuhi sifat hasil bagi sebuah suku dengan suku sebelumnya berurutan bernilai konstanta. Misalnya barisan geometri tersebut yaitu a,b, dan c maka c/b =b/a sama dengan konstanta. Hasil bagi suku yang berdekatan disebut disebut dengan rasio (r).

Misal ditemukan sebuah deret geometri
U1, U2, U3,…,Un-1, Un
Maka U2/U1, U3/U2,…, Un/Un-1 = r (konstan atau rasio)
Lalu bagaimana menentukan suku ke-n dari barisan geometri:

U3/U2 = r maka U3 = U2.r = a.r.r = ar2
Un/Un-1 = r maka Un = U_n-1. r = ar^n-2.r = ar^n-2+1 = ar^n-1
jadi dapat disimpulkan bahwa rumus suku ke-n baris geometri yaitu Un = ar^n-1
a= suku awal r rasio

Contoh Barisan Geometri

Agar kalian lebih memahami apa yang dimaksud dengan barisan geometri. Perhatikan contoh berikut ini:

3, 9, 27 , 81, 243, …

Barisan di atas merupakan contoh barisan geometri dimana setiap suku pada barisan tersebut merupakan hasil dari perkalian suku sebelumnya dengan konstanta 3. Maka dapat disimpulkan bahwa rasio pada barisan di atas adalah 3. rasio pada suatu barisan bisa dirumuskan menjadi:

r = ak+1/ak

Dimana ak yaitu sembarang suku dari barisan geometri yang ada. sementara ak+1 yaitu suku selanjutnya setelah ak. Untuk menentukan suku ke-n dari sebuah barisan geometri, kita bisa menggunakan rumus sebagai berikut:

U_n = ar^n-1

Dengan  a merupakan suku awal dan r ialah nilai rasio dari sebuah barisan geometri.

Contoh Soal dan Pembahasan Barisan Geometri

1. Sebuah Bakteri mampu melakukan pembelahan diri menjadi 4 setiap 12 menit. berapakah jumlah bakteri yang ada setelah 1 jam jika sebelumnya terdapat 3 buah bakteri?

Cara penyelesaian:

Diketahui:
a = 3
r = 4
n = 1 jam/12 menit = 60/12 = 5

Ditanya: U_5…?

Jawab:
U_n = arn-1
U₅ = 3 x 45-1
U₅ = 3 x 256 = 768 bakteri

Rumus deret Geometri

Deret geometri bisa diartikan sebagai jumlah dari n suku pertama pada sebuah barisan geometri. apabila suku ke-n dari suatu barisan geometri digambarkan dengan rumus: a_n = a₁r^n-1, maka deret geometrinya dapat dijabarkan menjadi:

S_n = a1 + a1r + a1r² + a1r³ + … + a1r^n-1

Jika kita mengalikan deret geometri di atas dengan -r, kemudian kita jumlahkan hasilnya dengan deret aslinya, maka kita akan memperoleh:

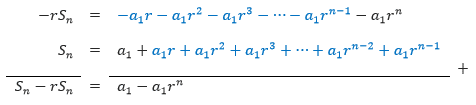
Setelah diperoleh S_n – rS_n = a₁ – a₁rⁿ maka kita bisa mengetahui nilai dari suku n pertama dengan cara sebagai berikut:

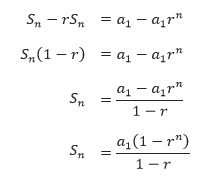
Berdasarkan kepada hasil perhitungan di atas, maka bisa disimpulkan bahwa rumus jumlan n suku pertama pada sebuah barisan geometri ialah:

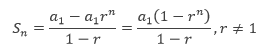
Contoh Soal Deret Geometri

1. Tentukanlah jumlah 8 suku pertama dari barisan geometri 2, 8, 32, ..

Cara penyelesaian:

Diketahui:
a = 2
r = 4
n = 8

Ditanya: S_8..?

S_n = a  (1-rⁿ) / (1-r)
S₈ = 2  (1-4⁸) / (1-4)
S₈ = 2  (1-65536)/ (-3)
S₈ = 2  (-65535)/ (-3)
S₈ = 2 x 21845
S₈ = 43690

Sisipan Barisan Geometri

Dalam barsan geometri terdapat sisipa. Misalnya antara p dan q ada sisipan k buah bilangan dan terjadi barisan geometri, maka rasio barisan geometri dapat dicari dengan rumus:

Suku Tengah Barisan Geometri

Apabila U1, U2,…,Un merupakan barisan geometri dengan n ganjil maka suku tengah barisan geometri tersebut dapat dicari dengan rumus berikut ini:

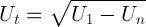
Deret Geometri Tak Hingga

Saat bola bekel dijatuhkan dari ketinggian 1 meter maka bola tersebut aka memantuk ketas sejauh 0,8 tinggi jatuh sebelumnya, lalu berapa jarak yang ditempuh bola bekel hingga berhenti?

Ini merupakan contoh deret geomerti tak hingga yaitu deret yang banyak sukunya tak terhingga. Jumlah suku dari deret tak hingga ada kemungkinan hingga atau tak hingga. Apabila deret tersebut hingga maka deret tersebut disebut deret konvergen dan Apabila tak hingga disebut deret divergen. Lebih jelasnya, apabila jumlah deret tak hingga menuju ke suatu harga tertentu yang berhingga maka disebut deret konvergen (mengerucut). Sebaliknya, deret geometri yang menuju bilangan tak hingga disebut deret divergen.

Deret tak hingga yang memilii rasio r ≥ 1 atau r ≤ 1 disebut deret divergen dan yang memiliki rasio -1< r < 1 disebut deret konvergen. Untuk menghitung deret tak hingga ada dua rumus tergantung pada nilai r.