Penjelasan Fungsi Komposisi, Aljabar Fungsi Dan Komposisi Fungsi Matematika

Penjelasan Fungsi Komposisi Aljabar Fungsi Dan Komposisi Fungsi Matematika, Akan menjelasakan lebih lengkap mengenai Fungsi komposisi, Aljabar Fungsi, Komposisi Fungsi dalam matematika serta rumus dan soal-soalnya.

Dengan demikian simak penjelasan di bawah ini agar kamu lebih memahami penjelasan berikut ini sehingga dapat menjad referensi dan memudahkan dalam mengerjakan soal.

Fungsi dan Sifat-sifatnya

1. Pengertian Fungsi

Suatu relasi dikatakan sebagai fungsi jika setiap unsur di daerah asai (domain = D) dipasangkan dengan tepat ke satu unsur di daerah kawan. Sebagai misal A dan B masing-masing merupakan himpunan. Reiasi fungsi (f) dari A ke B (f: A → B) dikatakan sebagai fungsi jika setiap anggota A dipasangkan dengan tepat ke satu anggota B.

2. Sifat-Sifat Fungsi

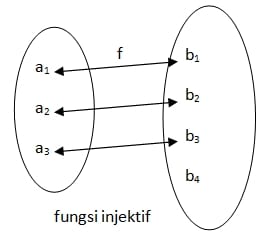
• Fungsi Injektif (Fungsi Satu-Satu)
  Fungsi f dari A ke B merupakan fungsi injektif jika anggota B dipasangkan dengan tepat ke satu anggota A, tetapi tidak semua anggota B harus mempunyai pasangan dengan anggota A. Dengan kata lain, fungsi f dari A ke B merupakan fungsi injektif jika a₁ , a₂ € D_f dengan a₁ ≠ a₂ maka f(a₁) ≠ f(a2). Df = daerah asal fungsi f.
  

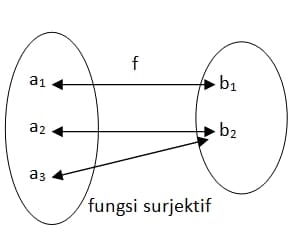
• Fungsi surjektif (Fungsi onto)
  Fungsi f dari A ke B merupakan fungsi surjektif jika setiap anggota B mempunyai pasangan dengan anggota A.
  

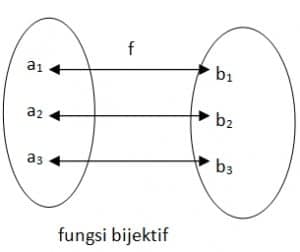
• Fungsi Bijektif (Fungsi Berkorespondensi Satu-Satu)
  Suatu fungsi dikatakan bijektif jika fungsi tersebut merupakan fungsi injektif sekaligus surjektif.
  

Aljabar Fungsi

1. Penjumlahan, Pengurangan, Perkalian, dan Pembagian Dua Fungsi

Jika f dan g merupakan fungsi, berlaku sifat-sifat aijabar fungsi sebagai berikut.

1. Penjumlahan fungsi : (f + g)(x) = f(x) + g(x)
2. Pengurangan fungsi: (f – g)(x) = f(x) – g(x)
3. Perkalian fungsi : (f . g)(x) = f(x) . g(x)
4. Pembagian fungsi : (^f/_g) (x) = ^f(x)/_g(x) . g(x) ≠ 0

2. Daerah Asal Fungsi

Diketahui f dan g merupakan fungsi dengan D_f = daerah asal f dan D_g = daerah asal g. Daerah asal operasi aljabar dua fungsi sebagai berikut.

1. Daerah asal fungsi (f + g)(x): D_{f + g} = Df ∩ Dg
2. Daerah asal fungsi (f – g)(x): D_{f -g} = Df ∩ Dg
3. Daerah asal fungsi (f . g)(x) : D_f.g = Df ∩ Dg
4. Daerah asal fungsi (^f/_g) (x) : D_f/g = Df ∩ Dg dengan g(x)  0

Komposisi Fungsi

1. Pengertian Komposisi Fungsi

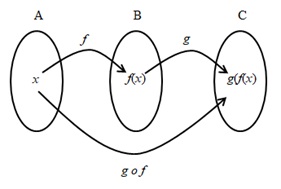
Jika f dan g merupakan fungsi, komposisi fungsi f dan g (ditulis f ₒ g) dirumuskan sebagai berikut.

(f ₒ g)(x) = f(g(x))

f ₒ g dibaca f bundaran g atau f komposisi g.
Artinya, mula-mula unsure x € D_g dipetakan oleh g ke g(x), kemudian g(x) dipetakan oleh f ke f(g(x)). Dengan cara yang sama diperoleh komposisi fungsi berikut.

(g ₒ f)(x) = g(f(x))
(f ₒ g ₒ h)(x) = f(g(h(x)))

2. Sifat-Sifat Komposisi Fungsi

1. Komposisi fungsi tidak bersifat komutatif.
   (f ₒ g)(x) ≠ (g ₒ f)(x)
2. Komposisi fungsi bersifat asosiatif.
   (f ₒ g ₒ h)(x) – (f ₒ (g ₒ h))(x) = ((f ₒ g) ₒ h)(x)
3. Dalam komposisi fungsi terdapat sebuah fungsi identitas, yaitu |(x) = x sehingga (f ₒ l)(x) = (I ₒ f)(x) = f(x)