Persamaan Lingkaran Matematika Rumus dan Pembahasan Lengkap Contoh Soal, Berikut akan memberikan penjelasan lengkap dari Persamaan Lingkaran dari rumus hingga pembahasan dan contoh soal.
Oleh sebab itu, pengertian Lingkaran adalah tempat kedudukan atau himpunan titik titik yang berjarak sama terhadap suatu titik tertentu. Titik tertentu tersebut dinamakan pusat lingkaran dan jarak yang tetap tersebut dinamakan jari-jari lingkaran.
Simak beriktu ini Persamaan Lingkaran Matematika Rumus dan Pembahasan Lengkap Contoh Soal.
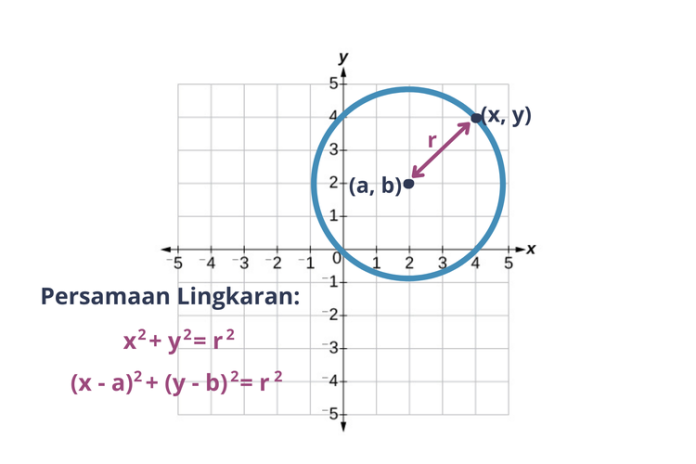
1. Persamaan Lingkaran dengan pusat O(0,0)
Jika titik A (x,y) terletak pada lingkaran yang berpusat di O makan OA= jari-jari lingkaran. Dengan menggunakan rumus jarak titik O (0,0) ke titik A (x,y) diperoleh
![]()
Persamaan lingkaran yang berpusat di (0,0) dan berjari-jari r dirumuskan sebagai berikut.
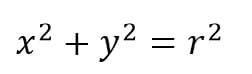
Tentukan persamaan lingkaran jika diketahui:
a. Pusatnya O (0,0) dan berjari-jari 10
b. Pusatnya O(0,00 dan melalui (8,-15)
Jawab.
a.Pusatnya O (0,0) dan berjari-jari 10 ,adalah
X2 + y2 = r2
X2 + y2 = 102
X2 + y2 = 100
Jadi, persamaan lingkarannya adalah X2 + y2 = 100
b. Pusatnya O(0,00 dan melalui (8,-15), adalah
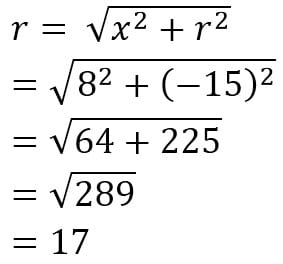
X2 + y2 = r2
X2 + y2 = 172
X2 + y2 = 289
jadi, persamaan lingkarannya adalah X2 + y2 = 289
2. Persamaan Lingkaran dengan pusat A (a,b)
Jika titik A (a,b) adalah pusat lingkaran dan titik B (x,y) terletak pada lingkaran maka jari-jari lingkaran r sama dengan jarak dari A ke B diperoleh
![]()
Persamaan lingkaran yang berpusat di P (a,b) dan berjari-jari dirumuskan sebagai berikut
(x – a)2 + (y – b)2 = r2
Tentukan persamaan lingkaran yang berpusat di (3,-2) dan melalui titik (5,4).
Jawab
(x – 3)2 + (y – (-2))2 = r2
(x – 3)2 + (y + 2)2 = r2 -> melalui (5,4)
(5 – 3)2 + (4 + 2)2 = r2
22 + 62 = r2
4 + 36 = r2
r2 = 38
jadi, persamaan lingkarannya adalah (x – 3)2 + (y + 2)2 = 38
3. Menentukan Pusat dan Jari Jari Lingkaran yang Persamaanya Diketahui
Bentuk umum persaman lingkaran yang berpusat di P 9a,b) dan berjari-jari r sebagai berikut.
X2 + y2 + 2Ax + 2By + C = 0
Pusat lingkaran: P(-A,-B)
Jari jari lingkaran : ![]()