Rumus dan Pembahasan Peluang, Permutasi, dan Kombinasi Lengkap Contohnya

Peluang Suatu Kejadian

Peluang atau probabilitas adalah kemungkinan sebuah kejadian dapat terjadi. Percobaan merupakan suatu proses yang dilakukan untuk kemudian memperoleh suatu hasil pengukuran, perhitungan, ataupun pengamatan. Himpunan dari semua hasil yang mungkin dari suatu percobaan disebut ruang sampel (S). Sehingga kejadian atau peristiwa merupakan himpunan bagian dari ruang sampel atau bagian dari hasil percobaan yang diinginkan.

Nilai probalitas antara 0 – 1. Kejadian yang mempunyai nilai probabilitas 0 adalah kejadian yang mustahil terjadi atau tidak mungkin terjadi. Sedangkan kejadian yang mempunyai nilai probalilitas 1 adalah kejadian yang pasti terjadi atau kejadian yang sudah terjadi.

Peluang atau probabilitas suatu kejadian A dapat terjadi dengan k dan mungkin hasil terjadi m cara sebagai:

$P(A) = \frac{k}{m}$

Frekuensi harapan suatu kejadian adalah hasil kali banyaknya percobaan dengan peluang kejadian yang akan terjadi dalam suatu percobaan atau:

Peluang Kejadian Majemuk

Peluang Gabungan Dua Kejadian

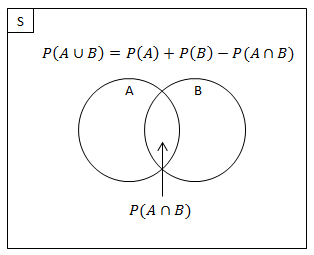
Dua buah kejadian A dan B dikatakan gabungan dua kejadian jika kejadian A dan B kejadian dapat terjadi bersamaan sehingga $A\cap B\neq {\O}$ dan menghasilkan rumus:

peluang kejadian majemuk

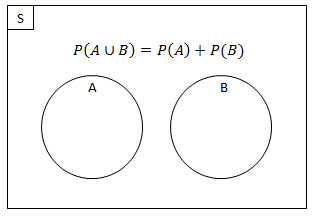
Peluang Gabungan Dua Kejadian yang Saling Lepas

Dua buah kejadian A dan B dikatakan gabungan dua kejadian saling lepas jika kejadian A dan B tidak mungkin terjadi bersamaan. Sehingga $A\cap B$ dan menghasilkan rumus:

- Iklan -

peluang gabungan saling lepas

Peluang Komplemen suatu Kejadian

Kejadian merupakan komplemen/ kebalikan A sehingga A danA’ merupakan kejadian saling lepas, maka $A\cap A' ={\O}$ . Sehingga menghasilkan rumus:

materi permutasi kombinasi komplemen

Peluang Kejadian Bersyarat

Dua kejadian disebut kejadian bersyarat jika munculnya kejadian pertama A mempengaruhi peluang munculnya kejadian kedua B. Maka peluang terjadinya kejadian B yang dipengaruhi oleh kejadian A ditulis dengan $P(B\mid A)$ . Bila $P(A\cap B)$ adalah peluang terjadinya A dan B , maka

$P(B\mid A) = \frac{P(A\cap B)}{P(A)}$

Contoh Soal Peluang dan Pembahasan

Contoh Soal 1

Dalam sebuah kotak berisi 7 bola merah dan 5 bola putih. Dari kota itu diambil 3 bola sekaligus. Peluang terambil sekurang-kurangnya 1 bola putih adalah

Pembahasan 1:

Karena harus terambil sekurang-kurangnya 1 bola putih maka peluang tidak terambilnya bola putih tidak termasuk itungan sehingga:

$P = 1 - P(O) = 1 - \frac{_7C_3 \times _5C_0}{_{12}C_3}$

$P = 1 - \frac{\frac{7 \times 6 \times 5 \times 4!}{3!(7 - 3)!} \times \frac{5!}{0!(5 - 0)!}}{\frac{12 \times 11 \times 10 \times 9!}{3!(12 - 3)!}}$

$P = 1 - \frac{35 \times 1}{220} = \frac{37}{44}$

Contoh Soal 2

Tentukanlah nilai n yang memenuhi persamaan

Pembahasan 2:

$3 \cdot \frac{(n + 1)!}{3!(n + 1 - 3)!} = 7 \cdot \frac{n!}{2!(n - 2)!}$

$3 \cdot \frac{(n - 1)n (n - 1)(n - 2)!}{(3.2.1)(n - 2)!} = 7 \cdot \frac{n(n - 1)(n - 2)!}{2 . 1(n -2)!}$

$3 \cdot \frac{(n + 1)n (n - 1)}{3.2.1} = \frac{7 \cdot n(n - 1)}{2.1}$

$\frac{3 . 2 . 1 (n + 1)n(n - 1)}{3 . 2 . 1 n(n - 1)} = 7$

$(n + 1) 7\overset{sehingga}{\rightarrow}n = 6$

Contoh Soal 3

Berapa banyak urutan yang dapat terjadi jika 5 bendera yang berwarna putih, merah, hijau, kuning, dan biru dipancang pada tiang-tiang dalam satu baris, dengan bendera putih selalu berada di salah satu ujung.

Pembahasan 3:

Karena bendera putih dipancang dalam salah satu ujung maka dengan 2 cara, sisa 4 bendera dapat diatur dalam $_4P_4$ cara, sehingga:

Jumlah urutan $= 2 \times _4P_4 = 2 \times (4 \times 3 \times 2 \times 1) = 48$ urutan.

Itulah penjelasan lengkap dari Peluang Permutasi dan Kombinasi lengkap dengan contoh-contohnya. Semoga materi di atas dapat membantu dan bermanfaat!