Rumus dan Penjelasan Sudut Pusat dan Sudut Keliling Lingkaran, BerikutPelajaran Sekolah akan memberikan penjelasan dan pembelajaran matematika yaitu Sifat Dan Rumus Sudut Pusat Dan Sudut Keliling Lingkaran yang meliputi pengertian dan rumus serta penjelasannya.
Dengan demikian simak berikut lebih lengkapnya
Pengertian Sudut Pusat dan Sudut Keliling
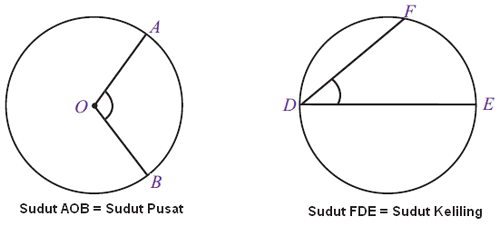
Sudut pusat adalah sudut dengan derajat tertentu yang dibentuk oleh dua buah jari-jari yang menghadap pada sebuah busur lingkaran. Sedangkan sudut keliling adalah sebuah sudut pada lingkaran yang dibentuk oleh dua buah tali busur. Jadi perbedaan utama antara sudut pusat dengan sudut keliling yaitu elemen pembentuknya, sudut pusat dibentuk oleh dua buah jari-jari sedangkan sudut keliling dibentuk oleh dua buah tali busur. Agar kalian lebih memahami perbedaan keduanya silahkan perhatikan gambar di bawah ini.
Sudut AOB = Sudut Pusat
Sudut FDE = Sudut Keliling
Hubungan Antara Sudut Pusat dengan Sudut Keliling Lingkaran
Sudut pusat dan sudut lingkaran yang memenuhi kriteria tertentu dapat memiliki hubungan.
“Jika terdapat sudut pusat lingkaran dan sudut keliling lingkaran yang menghadap pada tali busur lingkaran yang sama maka dua kali sudut lingkaran sama dengan nilai sudut pusat.”
Jika dibuat matematis:
Sudut Pusat = 2 x Sudut Keliling
atau sudut keliling sama dengan 1/2 dari sudut pusat.
Sifat Sudut Pusat dan Sudut Keliling Lingkaran
Tahukah kalian ternyata sudut pusat dan sudut keliling memiliki sifat-sifat khusus. Berikut penjelasannya.
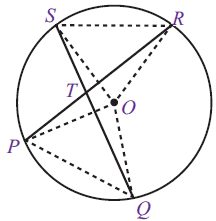
1. Sudut keliling yang menghadap diameter lingkaran selalu membentuk sudut 90 derajat atau biasa disebut dengan sudut siku-siku.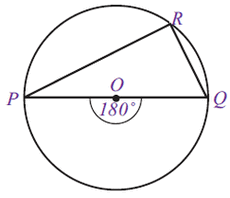
Sudut PRQ besarnya adalah 90 derajat.
2. Sudut keliling yang menghadap busur yang sama akan memiliki besar sudut yang sama pula.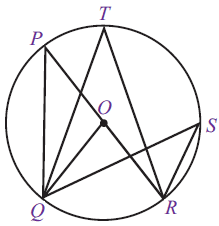
Menurut sifat di atas maka besarnya ∠ QPR = ∠ QTR = ∠ QSR
3. Sudut-sudut keliling yang saling berhadapan akan memiliki jumlah total sudut 180 derajat.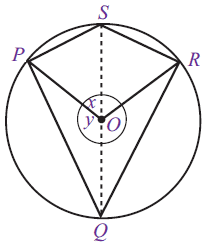
∠ PSR + ∠PQR = 180 derajat
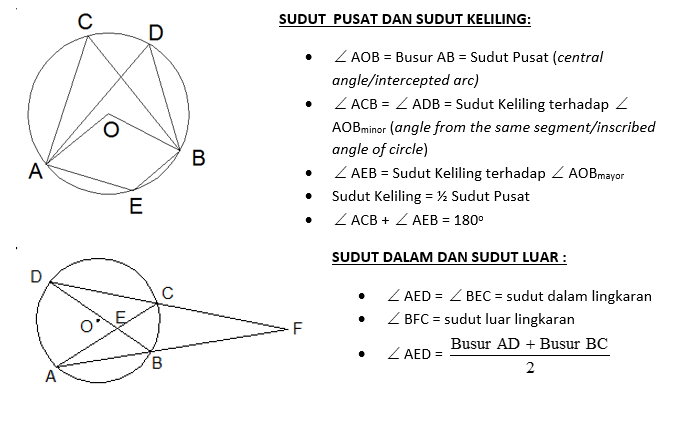
Sudut Diantara Dua Tali Busur
Soal yang melibatkan dua tali busur yang saling berpotongan sering kali cukup membingungkan. Jika perpotongan tepat pada garis lingkaran akan sangat mudah. Namun jika perpotongannya terjadi di dalam sebuah lingkaran atau di luar lingkaran akan cukup membingungkan.
a. Saling Berpotongan Di Dalam Lingkaran
Jika terdapat dua tali busur yang saling berpotongan di dalam sebuah lingkaran maka besar sudut antara dua tali busur yang berpotongan di dalam sebuah lingkaran tersebut sama dengan setengah kali dari jumlah sudut pusat yang tepat berada di depan dan dibelakannya. Perhatikan contoh berikut ini.
∠ PTS = ½ (∠ POS + ∠ QOR)
∠ STR = ½ (∠ SOR + ∠ POQ)
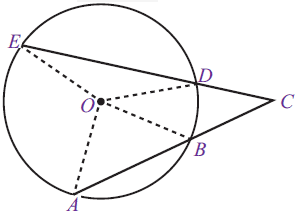
b. Saling Berpotongan Di Luar Lingkaran
Jika terdapat dua tali busur saling berpotongan di luar lingakaran maka besar sudut antara dua tali busur yang berpotongan di luar lingkaran ialah setengah kali selisih sudut pusat yang terletak diantara kedua tali busur tersebut.
∠ TRP = ½ ( ∠ TOP – ∠ SOP)
Itulah Rumus dan Penjelasan Sudut Pusat dan Sudut Keliling Lingkaran, semoga bermanfaat!
