Rumus Gerak Rotasi dan Contoh Soal, Serta Penjelasannya, Gerak rotasi yakni merupakan gerakan memutar dari suatu benda terhadap titik tertentu.
Dilansir dari laman Materibelajar.co.id, berikut ini penjelasan lengkap dari Rumus Gerak Rotasi dan Contoh Soal, Serta Penjelasannya. Simak di bawah ini
Pengertian Gerak Rotasi
Gerak rotasi yakni merupakan gerakan memutar dari suatu benda terhadap titik tertentu. Sebagai contoh yaitu gerak rotasi pada gasing. Pada gasing, titik yang menjadi acuan perputarannya yakni terdapar pada ujung tumpuan ketika gasing berputar. Lalu, apa sajakah besaran yang terlibat dalam gerak rotasi? Nah, kali ini akan kami bahas besaran-besaran yang terlibat dalam gerak rotasi diantaranya sebagai berikut :
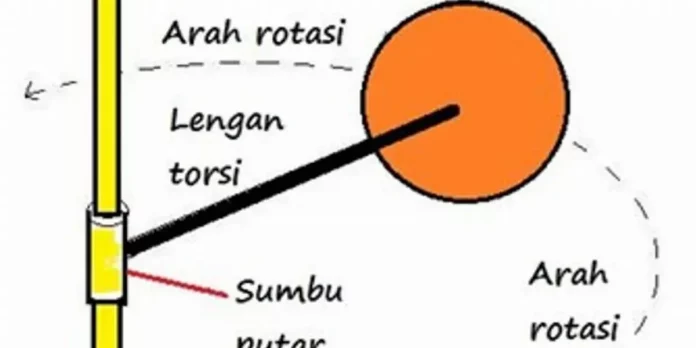
A. Torsi (Momen Gaya)
Torsi (Momen Gaya) yakni merupakan besaran yang menyebabkan terjadinya gerak rotasi . Adapun besaran ini disimbolkan dengan (T). Torsi adalah hasil kali antara gaya dengan lengannya. Lengan gaya adalah jarak tegak lurus antara sumbu rotasi dengan garis kerja gaya tersebut.
Adapun torsi dirumuskan sebagai berikut ini :
τ = r F sin Ѳ
Keterangan :
τ = momen gaya torsi (Nm)
r = lengan gaya (meter)
F = gaya (Newton)
e = sudut antara r dan F
B. Momen Inersia
Massa benda adalah ukuran kelembaman benda pada gerak lurus atau (gerak translasi). Jika menganalogikan hal itu, akan diperoleh besaran yang akan menentukan kelembaman benda gerak rotasi. Adapun besaran tersebut dinamakan momen inersia yang disimbolkan dengan ( / ) dan rumusnya seperti berikut ini.
|= m r2
Keterangan:
| = momen inersia ( kg m2 )
m = massa benda ( kg )
r = lengan gaya ( meter )
Adapun Nilai Momen Inersia pada sistem benda dengan jumlah lebih dari 1 yakni sebagai berikut.
Berdasarkan Hukum II Newton, keterkaitan antara gaya, massa, dan percepatan benda dirumuskan seperti berikut ini ;
F= ma
Adapun gaya tersebut yakni menjadi penyebab terjadinya gerak translasi, massa (m) adalah ukuran kelembaman gerak translasi, serta percepatan linear (a) adalah percepatan yang timbul dari gerak translasi.
Kalian sudah mengetahui bahwa torsi adalah penyebab gerak rotasi dan momen inersia (/) merupakan ukuran kelembaman pada gerak rotasi. Percepatan yang ditimbulkan gerak rotasi dinamakan percepatan sudut (a). Dengan begitu, Hukum II Newton untuk gerak rotasi dirumuskan seperti berikut ini.
τ = | α
Keterangan:
τ =torsi ( Nm )
| = momen inersia ( kg m2 )
α= percepatan sudut ( rad/s2 )
C. Momentum Sudut
Kemudian, momentum sudut (L) memiliki persamaan dengan momentum linear (p). Momentum linear adalah hasil kali antara massa dengan kecepatan suatu benda. Sedangkan momentum sudut merupakan hasil kali antara momen inersia dengan kecepatan sudut benda pada saat benda berputar. Secara matematis, momentum sudut dirumuskan seperti berikut ini.
L= | ω
Keterangan:
| = momen inersia ( kg m2 )
ω = kecepatan sudut ( rad/s )
L = momentum sudut ( kg m2/s )
Hukum II Newton untuk gerak rotasi dapat dinyatakan dalam rumus berikut.
Berdasarkan rumusan ini bisa dipahami bahwa perubahan torsi yang terjadi pada suatu benda yakni merupakan laju perubahan momentum sudutnya.
Selain dari rumusan di atas gerak rotasi menurut hukum II Newton dapat dinyatakan seperti berikut ini.
∑τ = │α
E. Hukum Kekekalan Momentum Sudut
Konsep Hukum Kekekalan Momentum Sudut yakni sebagai berikut.
“ Apabila torsi yang bekerja pada benda bernilai nol, jadi momentum sudut total benda yang berotasi besarnya konstan atau tetap ”. Persamaan yang berhubungan dengan hukum ini yakni:
F. Hukum Kekekalan Energi pada Gerak Translasi dan Rotasi
Rumus energi kinetik translasi, Sebagai berikut :

Rumus energi kinetik rotasi, Sebagai berikut :
Energi kinetik total dan benda, Sebagai berikut :
![]()
Energi total atau energi mekanik dirumuskan seperti berikut :
![]()
Contoh Soal
Pada baling-baling kipas angin berputar 25 rad/s. Apabila momen inersia kipas angin adalah 0,002 kg m2, Maka tentukan momentum sudut kipas angin tersebut !
Penyelesaian:
Diketahui:
I = o,oo2 kg m2
ω = 25 rad/s
Ditanyakan: L
Jawab:
L = I ω
= (oo,o,2 kg m2)(25 rad/s)
= o,o5 kg m2/s